EXAFS

NANO SKUPKI

 

PREPOZNAVANJE OBLIKE SKUPKOV

Analitični model, ki je bil razvit za krogelne skupke lahko razširimo tudi na druge oblike. Izberimo še dve karakteristični geometrijski obliki: valj s premerom D, ki je v eni dimenziji neskončno dolg ter plošča debeline D, ki je neskončna v dveh dimenzijah (slika 4.1). Med seboj bomo skupke lahko primerjali po karakterističnih dimenzijah D. Pri krogli in valju je to premer skupka, pri plošči pa njena debelina.

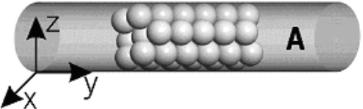
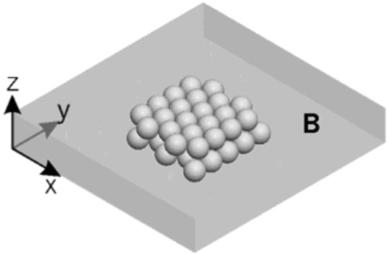
Slika 4.1: Shematski prikaz valjastega in ploščatega skupka s fcc kristalno strukturo. Na obeh slikah je prikazan le izsek skupka z le nekaj atomi. Valjasti skupek (A) je sestavljen iz vrst atomov v smeri , ploščati skupek (B) pa je sestavljen iz plasti atomov, ki so naložene ena na drugo v smeri .

Krogelni model lahko razširimo na ostale oblike, vendar bomo za lažje razumevanje ubrali drugo pot, kot jo je uporabil Borowski za krogle. Do enačbe (3.2) lahko pridemo tudi na naslednji način. Volumen dela skupka, ki je na sliki 3.3 označen s sivo barvo je v resnici presek dveh krogel s premerom D, pri čemer je središče druge krogle za vektor  premaknjeno od središča prve krogle (slika 4.2). Razmerje med volumnom preseka in volumnom cele krogle nas privede do iste enačbe (3.2).

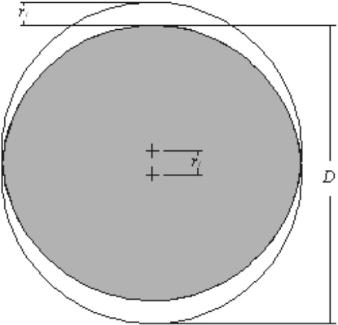
Slika 4.2: Shematski prikaz preseka (sivo) dveh krogel s premerom D, katerih središči sta med seboj razmaknjeni za razdaljo r. Razmerje med volumnom preseka in volumnom cele krogle je enako deležu sosedov .

Na enak način sem izpeljal še analitični model za valjaste in ploščate skupke. Ekvivalentno enačbo za delež sosedov v posamezni lupini v primeru valjastega skupka dobimo iz razmerja med volumnom preseka dveh valjev in volumnom celega valja:      

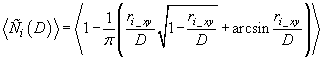(4.1)

kjer je D premer valja,  projekcija vektorja  na ravnino xy, celoten izraz pa je povprečen čez vse možne smeri za . Enačba velja samo za dovolj velike premere D³ ri_xy. V nasprotnem primeru je delež sosedov enak nič.

Enačbo za ploščate skupke pa dobimo z razmerjem volumna preseka dveh plošč in volumna cele plošče:          

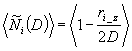(4.2)

kje je D debelina plošče,projekcija vektorja na os , celoten izraz pa je povprečen čez vse možne smeri za . Podobno kot prej velja enačba le za dovolj velike skupke. V nasprotnem primeru je delež sosedov enak nič.

Veljavnost analitičnega modela za valjaste skupke lahko preverimo z numerično izračunanimi deleži sosedov za različno velike skupke. Uporabil sem že prej omenjeni algoritem, ki je najprej izračunal koordinate atomov zloženih v eno samo vrsto, ter nato dodajal okoli teh atomov nove plasti atomov do izbranega premera skupka tako, da se je obdržala valjasta oblika skupka, kot je prikazano na sliki 4.1a. Nato je algoritem izračunal deleže sosedov za prve štiri koordinatne lupine na enak način, kot pri krogelnem skupku. Model za valjaste skupke je dober za skupke s premerom večjim od 20 Å, pri manjših skupkih pa pride do odstopanja od numerično izračunanih vrednosti, ker so odstopanja od valjaste oblike že tako velika, da jih ne moremo več aproksimirati z valjem (slika 4.3).

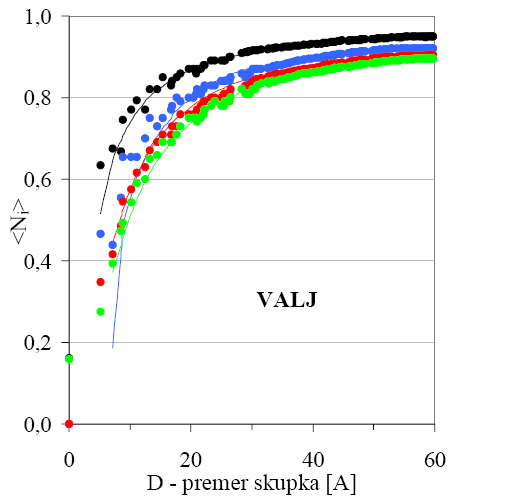
Slika 4.3: Primerjava analitičnega modela (črte) z numerično izračunanimi vrednostmi (pike) za deleže sosedov v prvi (črno), drugi (modro), tretji (rdeče) ter četrti (zeleno) koordinatni lupini v valjastih skupkih s kristalno strukturo fcc a=3,55Å različnih velikosti.

Koordinate atomov v ploščatem skupku je program izračunal tako, da je zlagal ravnine gosto zloženih atomov po plasteh (slika 4.1b). Najmanjši ploščati skupek ima eno samo plast gosto zloženih atomov ter debelino 0, ker velikosti atomov samih ne upoštevamo. Model za ploščate skupke je popolnoma točen za vse ploščate skupke od dveh plasti naprej (slika 4.4).

Podobno kot pri krogelnih skupkih lahko tudi pri valjastih ter pri ploščatih določimo največjo velikost, pri kateri še lahko razlikujemo med dvema skupkoma, ki se po premeru med seboj razlikujeta za 1Å, če je delež sosedov določen na 0,03 natančno. S primerjanjem deležev prvih sosedov lahko tako ločimo valjaste skupke s premerom manjšim od 8Å, za nadaljnje sosede pa je metoda bolj občutljiva. Če primerjamo na primer deleže četrtih sosedov lahko ločimo skupke s premerom manjšim od 9Å. Kot pri krogelnih skupkih tako tudi pri valjastih analitični model ne opiše natančno numeričnih vrednosti pri omenjenih velikostih, zato je ta ocena le grob približek.

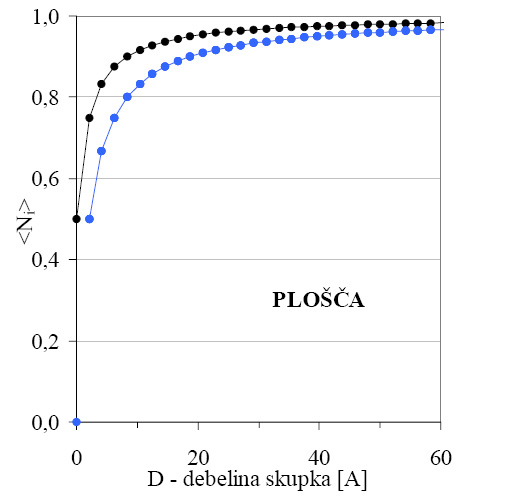
Slika 4.4: Enako kot pri sliki 4.3. Deleži sosedov v prvi (črno), drugi, tretji in četrti lupini (modro) v ploščatem skupku. Deleži za drugo, tretjo in četrto lupino se popolnoma prekrivajo, zato so vsi prikazani z istim nizom.

Pri ploščatih skupkih lahko po enakem kriteriju s primerjanjem deležev prvih sosedov razlikujemo skupke z debelino manjšo od 7Å, s primerjanjem deležev četrtih sosedov pa skupke z debelino manjšo od 13Å.V nasprotju s krogelnimi in valjastimi skupki nam analitični model natančno opiše numerične vrednosti, zato je omenjena ocena zanesljiva.

Funkcijska odvisnost deleža sosedov od karakteristične dolžine D je drugačna za vsako izmed oblik in za vsako izmed koordinatnih lupin. Tudi razmerje med deleži sosedov različnih koordinatnih lupin je drugačno za vsako obliko in tu se pokaže možnost ločevanja med posameznimi oblikami.

 

 

 

 

E-mail:iztok.arcon@p-ng.si Last change: 20-Apr-2006